What do the following scales have in common?
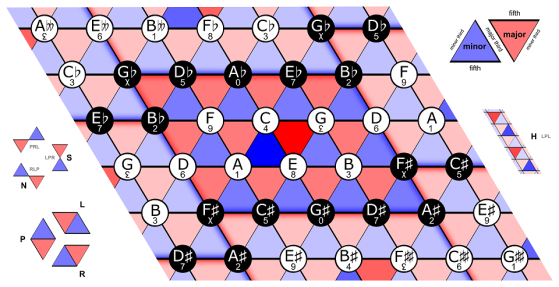
The answer to this riddle is (in my humble opinion) a really neat compositional tool. Aside from two of these scales being the common major and minor, the overall relationship doesn’t seem very obvious at first. The first thing I need to introduce to demonstrate how these scales relate to each other is the Tonnetz Lattice
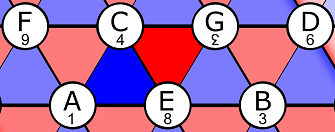
I want to specifically point out that in this diagram (as shown in the key at the upper right) ascending perfect fifths go to the right; ascending major thirds go down to the right; and ascending minor thirds go ascending up to the right. Using this diagram, we can outline shapes that contain specific sets of notes. The shape I want to emphasize is the outline containing the perfect fifths of F-C-G-D and below it, A-E-B, which together forms a major scale and a trapezoid.
The Tonnetz Lattice is handy such that once a particular shape is decided upon, moving it around the lattice (without rotating it or otherwise changing shape) results in maintaining the same quality of intervals between notes. Thus, major scales in F or G or B (et cetera) have the same shape.
Triangles in this lattice correspond to major and minor triads. My particular choice of shape results in three major triads and two minor triads. Note that the D minor triad in C major isn’t included in my trapezoid. If I did include it, depending on the details of a particular tuning system, the two Ds at either end of the parallelogram may or may not actually be the same pitch. In 12-note equal temperament (12ET), they are the same. For now, my explanation here is simpler if I leave out a D minor triangle. Also note the following:
– My chosen trapezoid has exactly 7 “nodes” which translate to at most 7 musical notes.
– The 3 major triads (triangles pointing down) are “primary” triads.
– The 2 minor triads (triangles pointing up) are “secondary” triads.
– Octave equivalence applies. The details of this lattice can change if the scale repetition interval changes.
– “Primary” and “secondary” in this context seems to not be as distinct in scale structure as the terminology implies. The particular direction of the triangles are basically equivalently important, but I’ll keep the classical terminology to keep things simple to follow.
Returning to the original riddle, the above list of scales is what results when I modify the Tonnetz Lattice, where the major third “down and to the right” becomes some other interval, and the minor third “up and to the right” becomes whatever is needed to result in a perfect fifth being maintained for the “directly to the right” direction. The following fleshes this result out in more detail. My informal descriptions work such that “Fifth/minor second” means that the perfect fifth goes to the right, and the minor second goes down and to the right – which results in the remaining interval up and to the right being the difference between a fifth and a minor second, or a tritone. “Primary” and “secondary” triads maintain the same meaning, being the same triangles in the same positions as were in our major scale, with the new resulting interval structures.
Some observations:
– Most of these scales are not modes of each other in 12ET.
– Some scales have notes repeated. This means that in 12ET, that note appears twice in the trapezoid. In other tuning systems, this can just mean the two notes are close to each other, not necessarily identical. But, it’s also interesting how this process can sometimes but not always result in 12ET scales that contain fewer than 7 distinct notes.
– Changing the interval structure can drastically change which notes are “close” to others. Not only does this apply to how doubled notes appear as noted above, but remember in the original Tonnetz Lattice that two Ds appear on and near opposite ends of my chosen trapezoid. Change the intervals, and those two notes may be wildly different pitches.
– You can conduct this exercise for any shape in the lattice that contains any number of triangles and nodes, not just my “major scale” trapezoid.
– If you add both “D” nodes to the shape, this results in 8 nodes, which can result in some 8-note scales, not just 7-note scales with 3 primary triads and 3 secondary triads.
– You can extend this lattice to more dimensions, and with other than just triangular structures.
– All of my scales assume a perfect fifth as the “to the right” interval, but this can change too. For example, a “major third/major second” interval scheme with my chosen trapezoid results in a 12ET whole-tone scale.